Let’s use this result and Snell’s law to determine the entrance cone for light rays incident on the face of a clad fiber if the light is to be trapped by total internal reflection at the core-cladding interface in the fiber.

Example 3

A step-index fiber 0.0025 inch in diameter has a core index of 1.53 and a cladding index of 1.39. See drawing. Such clad fibers are used frequently in applications involving communication, sensing, and imaging.



What is the maximum acceptance angle Ɵm for a cone of light rays incident on the fiber face such that the refracted ray in the core of the fiber is incident on the cladding at the critical angle?

Solution: First find the critical angle Ɵc in the core, at the core-cladding interface. Then, from geometry, identify θr and use Snell’s law to find Ɵm.

(1) From Equation 3-3, at the core-cladding interface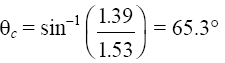



(2)From right-triangle geometry, Ɵr = 90 − 65.3 = 24.7°

(3)From Snell’s law, at the fiber face,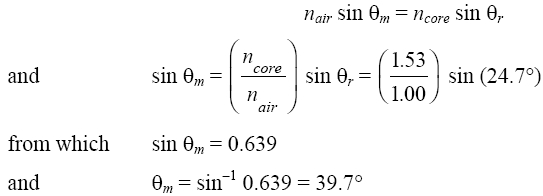



Thus, the maximum acceptance angle is 39.7° and the acceptance cone is twice that, or 2 θm = 79.4°. The acceptance cone indicates that any light ray incident on the fiber face within the acceptance angle will undergo total internal reflection at the core-cladding face and remain trapped in the fiber as it propagates along the fiber.