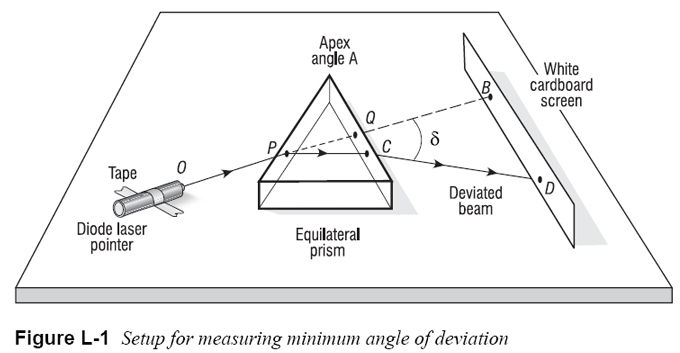
2. As you rotate the prism relative to the incident laser beam, the laser spot D on the screen moves, so the angle of deviation δ will become larger or smaller. By experimentation, determine the smallest angle of deviation (δm) between an original beam direction OPQB and the deviated beam CD. (It should be clear that the farther the screen is from the prism the more precise will be your determination of δm, since small changes in spot D will then be more exaggerated.)

3. When you have achieved the minimum angle for δ, carefully tape the prism in place. Trace the prism edges on the paper, the straight segments OP and QB along the original direction, and the segment CD. (Note: Location of laser spots Q, C on the exit face of the prism and B, D on the screen are needed to be able to draw segments QB and CD.) With the line segments drawn, remove the prism and measure the minimum angle δm with a protractor. Complete a ray trace of the incident beam through the prism, deviated at angle δm. Is the segment DC parallel to the prism base? Should it be?

4. Record the measured angle δm and the apex angle A. Use the formula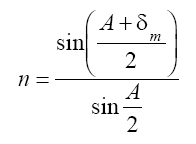

to calculate the index of refraction n. Compare your value with values given in Table 3-1. Does it agree with any value given there? What is your best guess for the prism material?

B. Total Internal Reflection (TIR)

(When you have finished this part, you will have three different traces of laser light interacting with right-angle prisms, all on an 11" × 17" sheet of white tracing paper.

1. Set a right-angle prism on one of its parallel sides on a sheet of 11" × 17" white tracing paper. Tape the paper and prism in position. Shine a diode laser beam onto an appropriate face of the prism so that it undergoes total internal reflection (TIR) and exits the prism at 90° to its original direction of entry. Use index cards as a screen to “locate” the laser beam