Using the small-angle approximation, the angles α, α′, and ϕabove can be replaced by their tangents, yielding 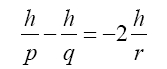
Note that we have neglected the axial distance VQ, small when ϕ is small. Cancellation of h produces the desired relationship, 
If the spherical surface is chosen to be concave instead, the center of curvature will be to the left. For certain positions of the object point O, it is then possible to find a real image point, also to the left of the mirror. In these cases, the resulting geometric relationship analogous to Equation 3-5 consists of the same terms, but with different algebraic signs, depending on the sign convention employed. We can choose a sign convention that leads to a single equation, the mirror equation, valid for both types of mirrors. It is Equation 3-6. 
2. Sign convention. The sign convention to be used in conjunction with Equation 3-6 and Figure 3-18 is as follows.
- Object and image distances p and q are both positive when located to the left of the vertex and both negative when located to the right.
- The radius of curvature r is positive when the center of curvature C is to the left of the vertex (concave mirror surface) and negative when C is to the right (convex mirror surface).
- # Vertical dimensions are positive above the optical axis and negative below.
In the application of these rules, light is assumed to be directed initially, as we mentioned earlier, from left to right According to this sign convention, positive object and image distances correspond to real objects and images, and negative object and image distances correspond to virtual objects and images. Virtual objects occur only with a sequence of two or more reflecting or refracting elements.
3. Magnification of a mirror image. Figure 3-19 shows a drawing from which the magnification—ratio of image height hi to object height ho—can be determined. Since angles ϴi, ϴr, and α are equal, it follows that triangles VOP and VIP' are similar. Thus, the sides of the two triangles are proportional and one can write
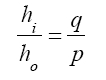
This gives at once the magnification m to be
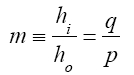
Page: 12345678910111213141516171819202122232425262728293031323334353637383940
| Eyes carePhysicianBate's booksTechnologyForumLaser corre.Blues under eyesburning in the eyesanother diseasesMedical mistery Naturally eyesight correction. No laser eye surgery. Restore eyesight. Vision correction. |




