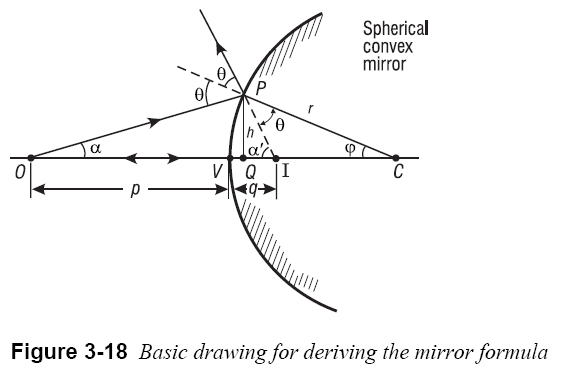
The mirror shown in Figure 3-18 is convex with center of curvature C on the right. Two rays of light originating at object point O are drawn, one normal to the convex surface at its vertex V and the other an arbitrary ray incident at P. The first ray reflects back along itself; the second reflects at P as if incident on a plane tangent at P, according to the law of reflection. Relative to each other, the two reflected rays diverge as they leave the mirror. The intersection of the two rays (extended backward) determines the image point I corresponding to object point O. The image is virtual and located behind the mirror surface.
Object and image distances measured from the vertex V are shown as p and q, respectively. A perpendicular of height h is drawn from P to the axis at Q. We seek a relationship between p and q that depends on only the radius of curvature r of the mirror. As we shall see, such a relation is possible only to a first-order approximation of the sines and cosines of angles such as αand ɸ made by the object and image rays at various points on the spherical surface. This means that, in place of expansions of sin ɸand cos ɸin series as shown here, 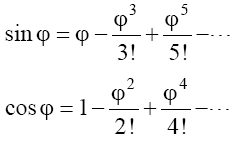
we consider the first terms only and write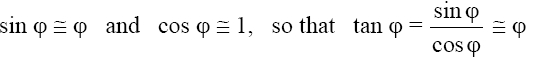
These relations are accurate to 1% or less if the angle ɸis 10° or smaller. This approximation leads to first-order (or Gaussian) optics, after Karl Friedrich Gauss, who in 1841 developed the foundations of this subject. Returning now to the problem at hand—that of relating p, q, and r— notice that two angular relationships may be obtained from Figure 3-18, because the exterior angle of a triangle equals the sum of its interior angles. Thus, 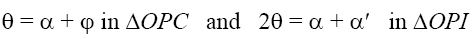
which combine to give 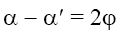
Page: 12345678910111213141516171819202122232425262728293031323334353637383940
| Eyes carePhysicianBate's booksTechnologyForumLaser corre.Blues under eyesburning in the eyesanother diseasesMedical mistery Naturally eyesight correction. No laser eye surgery. Restore eyesight. Vision correction. |




