Example 6
The passenger-side mirror on an automobile is a convex mirror. It provides the driver with a wide field of view, but significantly reduced images. Assume that object OP is part of an automobile trailing the driver’s car. See diagram below. Use three key rays to locate the reduced, virtual image of the trailing auto.
Solution: Using key rays 1, 2, and 3 incident on the mirror from point P on object OP, in conjunction with points C and F, draw the appropriate reflected rays, as show below, to locate P' on image IP'. 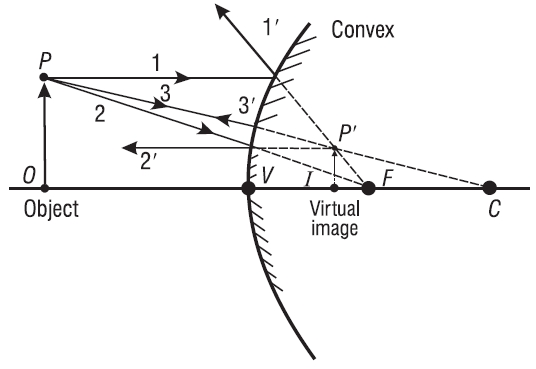
The three reflected rays 1', 2', and 3' diverge after reflection. They appear to come from a common point P′ behind the mirror. This locates virtual image IP′, reduced in size, about one-third as large as object OP. As a result, drivers are always cautioned that images seen in the passenger-side mirror are actually NEARER than they appear to be.
C. Mirror formulas for image location
In place of the graphical ray-tracing methods described above, we can use formulas to calculate the image location. We shall derive below a “mirror formula” and then use the formula to determine image location. The derivation is typical of those found in geometrical optics, and is instructive in its combined use of algebra, geometry, and trigonometry. (If the derivation is not of interest to you, you may skip to the next section, where the derived formula is used in typical calculations. Be sure, though, that you learn about the sign convention discussed below.)
1. Derivation of the mirror formula. The drawing we need to carry out the derivation is shown in Figure 3-18. The important quantities are the object distance p, the image distance q, and the radius of curvature r. Both p and q are measured relative to the mirror vertex, as shown, and the sign on r will indicate whether the mirror is concave or convex. All other quantities in Figure 3-18 are used in the derivation but will not show up in the final “mirror formula.”
Page: 12345678910111213141516171819202122232425262728293031323334353637383940
| Eyes carePhysicianBate's booksTechnologyForumLaser corre.Blues under eyesburning in the eyesanother diseasesMedical mistery Naturally eyesight correction. No laser eye surgery. Restore eyesight. Vision correction. |




