In addition, the numerical aperture is closely related to the acceptance angle discussed in Example 3 for both graded-index and step-index optical fibers, as will be shown in Module 1-7, Optical Waveguides and Fibers. Since the rays entering the fiber face are in air, the numerical aperture N.A. is equal simply to N.A. = sin ɑ.
It is shown in most basic books on optics (see references listed at end of this module) that image brightness is dependent on values of the f-number or numerical aperture, in accordance with the following proportionalities: 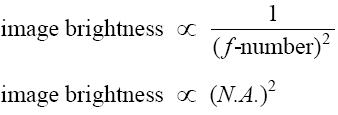
In summary, one can increase the light-gathering power of a lens and the brightness of the image formed by a lens by decreasing the f-number of the lens (increasing lens diameter) or by increasing the numerical aperture of the lens (increasing the refraction index and thus making possible a larger acceptance angle).
C. Image location by ray tracing
To locate the image of an object formed by a thin lens, we make use of three key points for the lens and associate each of them with a defining ray. The three points are the left focal point F, the right focal point F', and the lens vertex (center) V. In Figure 3-25 the three rays are shown locating an image point P′ corresponding to a given object point P, for both a positive and a negative lens. The object is labeled OP and the corresponding image IP'. The defining rays are labeled to show clearly their connection to the points F, F', and V. In practice, of course, only two of the three rays are needed to locate the desired image point. Note also that the location of image point P' is generally sufficient to sketch in the rest of the image IP', to correspond with the given object OP. 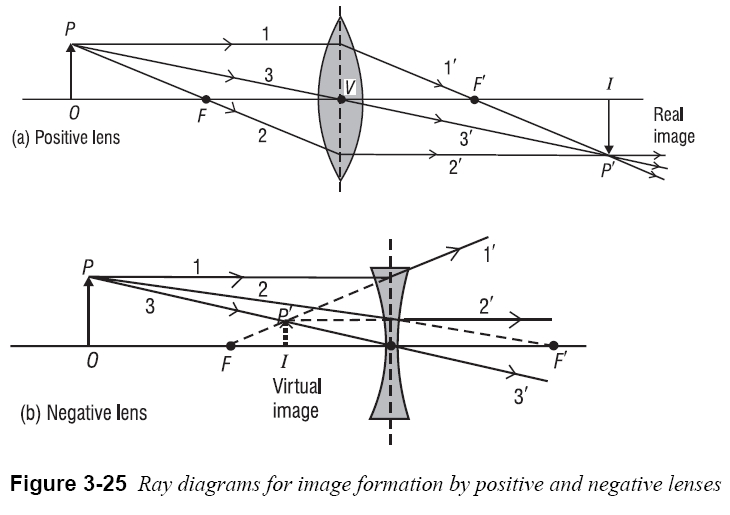
Page: 12345678910111213141516171819202122232425262728293031323334353637383940
| Eyes carePhysicianBate's booksTechnologyForumLaser corre.Blues under eyesburning in the eyesanother diseasesMedical mistery Naturally eyesight correction. No laser eye surgery. Restore eyesight. Vision correction. |




