(d) Since the sun is very far away, its light is collimated (parallel rays) as it strikes the lens and will come to a focus at the lens focal point. Thus, one should hold the lens about 16.5 cm from the index card to form a sharp image on the card.
Example 9
A two-lens system is made up of a converging lens followed by a diverging lens, each of focal length 15 cm. The system is used to form an image of a short nail, 1.5 cm high, standing erect, 25 cm from the first lens. The two lenses are separated by a distance of 60 cm. See accompanying diagram. (Refer to Figure 3-26 for a ray-trace diagram of what’s going on in this problem.) 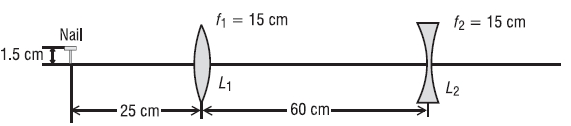
Locate the final image, determine its size, and state whether it is real or virtual, erect or inverted.
Solution: We apply the thin lens equations to each lens in turn, making use of the correct sign convention at each step. 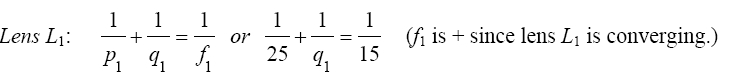
q1 = +37.5 cm (Since the sign is positive, the image is real and located 37.5 cm to the right of lens L1. 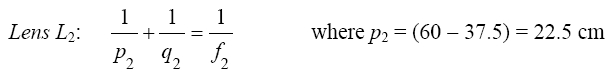
Since the first image, a distance q1 from L1, serves as the object for the lens L2, this object is to the left of lens L2, and thus its distance p2 is positive. The focal length for L2 is negative since it is a diverging lens. So, the thin lens equation becomes 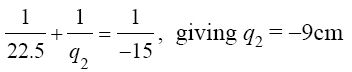
Since q2 is negative, it locates a virtual image, 9 cm to the left of lens L2. (See Figure 3-26.)
The overall magnification for the two-lens system is given by the combined magnification of the lenses. Then 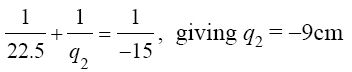
Thus, the final image is inverted (since overall magnification is negative) and is of final size(0.6 × 1.5 cm) = 0.9 cm.
Page: 12345678910111213141516171819202122232425262728293031323334353637383940
| Eyes carePhysicianBate's booksTechnologyForumLaser corre.Blues under eyesburning in the eyesanother diseasesMedical mistery Naturally eyesight correction. No laser eye surgery. Restore eyesight. Vision correction. |




